Expected Mean Highest Groundwater Level (EMHGL) 2016

Link to contact information

Methodology

Different methodologies were applied for the two areas glacial valley and Panke valley.

Glacial valley

For the area of the Berlin glacial valley, the EMHGL map was computed using a numerical groundwater flow model. This was necessary because due to the long-standing and sometimes strong anthropogenic influence on the groundwater surface, the computation of such a map is not possible in the sense of the above EMHGL definition solely on the basis of measuring groundwater levels and then calculating the mean.

The basis of the EMHGL model consists of the model which has already been used for developing the map of the expected highest groundwater level (EHGL). This model is described in Limberg, Hörmann & Verleger (2010) and is summarised here:

The numerical model, for which the software system MODFLOW was used, is designed to encompass the entire area of Berlin (Figure 4).

Fig. 4: Area of the groundwater flow model for developing the EHGL map and the EMHGL map for the Berlin glacial valley

Fig. 4: Area of the groundwater flow model for developing the EHGL map and the EMHGL map for the Berlin glacial valley

Image: Umweltatlas Berlin

The area of the Berlin glacial valley is vertically divided into several model layers, of which the uppermost represents the – here usually unconfined – main aquifer, whose EMHGL is to be calculated (see Figure 5).

Fig. 5: North-South section with vertical discretisation of the numerical groundwater flow model

Fig. 5: North-South section with vertical discretisation of the numerical groundwater flow model

Image: Umweltatlas Berlin

Horizontally, the model is divided into rectangular cells. The cell size varies between 50 × 50 and 100 × 100 metres.

This flow model was calibrated and verified using hydraulically stationary calculations. The groundwater levels measured in 2004 (calibration) and 2001 (verification) were used for this purpose. The plausibility of the EHGL model based on this was checked very successfully by means of measured highest groundwater levels (cf. also description of the EHGL map).

For the computational simulation of the EMHGL, compared to that of the EHGL, the conditions new groundwater formation and water levels of the receiving waters (Spree, Havel and their tributaries) were changed. In accordance with the objective, mean highest water levels (MHWLs) were specified as water levels. The time series 1960 to 2009 was used for determining the MHWL. The long-term mean new groundwater formation and its local distribution in the Berlin city area with its strong urban character are not known down to the last detail despite many efforts to determine them. The only assertion that can be made about the new groundwater formation which, together with the recipient heights, gives rise to the mean highest groundwater level, is that it must be lower than in the case of the highest groundwater level. For this reason, calculations were carried out using different degrees of reduced new groundwater formation. The aim was the best possible adaptation to the mean highest groundwater levels calculated from observation well levels of groundwater measuring points that are preferably without influence from groundwater extractions or discharges.

In several steps, 103 suitable hydrographs were selected from more than several thousand, from existing and also no longer existing groundwater measuring points for which data was available until 2010 at the State Geological Service. The hydrographs fulfil the following criteria:

  • filtration distance of the groundwater measuring points in the main aquifer;
  • groundwater level measured at least during the ten years before 2010;
  • no measurement gaps of more than half a year in the period for which the mean highest groundwater level is calculated;
  • no discernible unnaturally large fluctuations in the period under consideration.

The location of the groundwater measuring points whose MHGL values were used as target values for the modelling is represented in Figure 6. According to both the EMHGL and the EHGL definitions, all model computations have in common that neither groundwater extractions nor discharges occur.

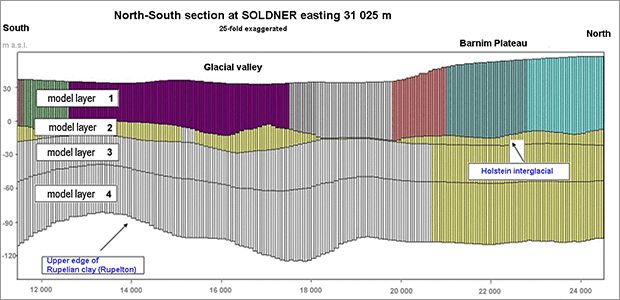
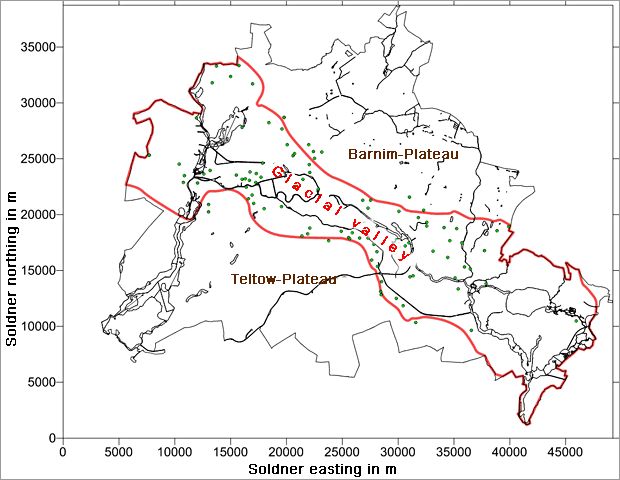
Fig. 6: Location of the 103 groundwater measuring points used for the EMHGL model adaptation

Fig. 6: Location of the 103 groundwater measuring points used for the EMHGL model adaptation

Image: Umweltatlas Berlin

The groundwater surface of the computational variant with the best adaptation to these target values corresponds to the EMHGL map. As an example, Figure 7 shows the hydrograph of a groundwater measuring point with the MHGL for the period 1998 to 2015 and the EMHGL calculated using the model. Here the EMHGL lies 0.13 m above the MHGL.

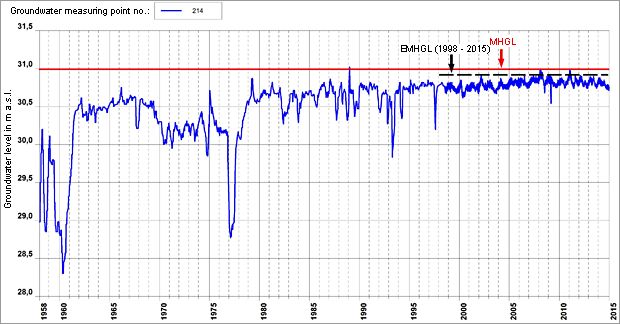
Fig. 7: Hydrograph of the groundwater measuring point 214 with recorded mean highest groundwater level (MHGL) for the period 1998 to 2005 and modelled expected mean highest groundwater level (EMHGL).

Fig. 7: Hydrograph of the groundwater measuring point 214 with recorded mean highest groundwater level (MHGL) for the period 1998 to 2005 and modelled expected mean highest groundwater level (EMHGL).

Image: Umweltatlas Berlin

In 2014, the groundwater flow model was updated for the EMHGL since partial revisions were carried out in the eastern area of the EHGL model. Measurement series up to 2014 are thus also taken into account.

Panke valley

No EHGL map calculated with a suitable groundwater flow model was available as a basis for developing the map of the expected mean highest groundwater level (EMHGL) in the area of the Panke valley and its transition to the glacial valley. Here the EHGL map was calculated from augmented HGL values from a total of 105 groundwater measuring points that have measurement series until 2014, using the programme SURFER (cf. explanation of the EHGL map).

In order to prevent the EMHGL map from contradicting the EHGL map (by definition, the EMHGL must be below the EHGL everywhere), the map of the expected mean highest groundwater level was created analogously. The same groundwater measuring points as for the EHGL map served as sampling points.

Methodologically, the development of the EMHGL map is structured along the following steps:

  • hydrograph analysis,
  • statistical analyses of the groundwater levels,
  • specification of the EMHGL values for 105 groundwater measuring points,
  • calculation of the EMHGL distribution and map representation.

The hydrograph analysis showed that the artificial influence on groundwater levels before 1990 is for the most part too strong for an MHGL for whose calculation these data were also taken into account to be regarded as the expected mean highest groundwater level. Likewise, the data from before 1990 were not taken into account for the EHGL map because of the strong influence. Moreover, the hydrographs from the early 2000s on show a tendency towards higher groundwater levels than in the 1990s, which can also be verified statistically.

As an example, Figure 8 shows the hydrograph of the groundwater measuring point no. 293 with the MHGL values for the entire period under consideration from 1990 to 2014 (MHGL90-14), the one from 1990 to 2001 (MHGL90-01) and the one from 2002 to 2014 (MHGL02-14). It is typical that the MHGL for the period from 2002 to 2014 is considerably higher than the one for the period from 1990 to 2001 and, moreover, that the history of groundwater levels is better documented through mostly daily measurements. For these reasons, only the MHGL values of the period 2002 to 2014 were used for computing the EMHGL map.

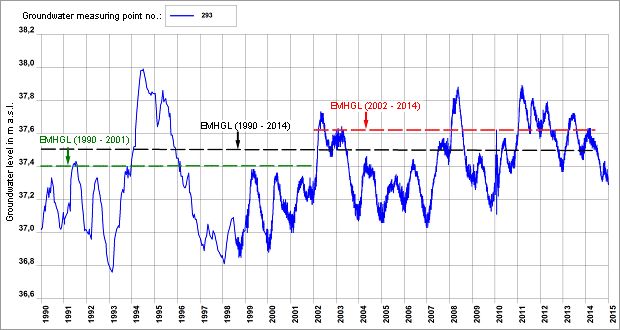
Fig. 8: Hydrograph of the groundwater measuring point no. 293 with the MHGL values for the periods 1990 to 2014 (black), 1990 to 2001 (green) and 2002 to 2014 (red)

Fig. 8: Hydrograph of the groundwater measuring point no. 293 with the MHGL values for the periods 1990 to 2014 (black), 1990 to 2001 (green) and 2002 to 2014 (red)

Image: Umweltatlas Berlin

Of the total of 105 groundwater measuring points on which the map of the expected highest groundwater level is based, 67 still existed in 2014. That is, for 38 measuring points, no or no sufficient groundwater level data are available for calculating the required MHGL for the period 2002 to 2014, but for the period 1990 until 2001 data are available, at least with some restrictions (e.g. lower measuring frequency). In order to obtain a grid of sampling points as dense as the one for the EHGL map, the MHGLs of these 38 measuring points were estimated for the period 2002 to 2014. By means of correlation analyses between different quantities obtained from the hydrographs, a significant relationship between the EMHGL for the period 2002 to 2014 (EMHGL 02-14), the mean value of the measurements between 1990 and 2001 (MGL 90-01) and the standard deviation of the measurements between 1990 and 2001 (s 90-01) was found.

With an increment of 20 cm selected to account for the uncertainties inherent in this procedure, the following formula for calculating the desired EMHGL 02-14 is obtained:

EMHGL 02-14 = 2.43 * s 90-01 + 0.13 + MGL 90-01

with

EMHGL 02-14 :desired expected mean highest groundwater level

s 90-01 :standard deviation of the measurements between 1990 and 2001

MGL 90-01 :mean value of the measurements between 1990 and 2001

According to this method, the MHGL values for the 38 groundwater measuring points mentioned above were estimated by calculation. As desired, the MHGL values for 105 measuring points are thus available.

Based on these 105 MHGL values and on another 15 sampling points that were specified at the border to the EMHGL map for the glacial valley in order to ensure consistent continuity with that map, the distribution of the EMHGL was calculated (without taking the surface waters into account) by means of the software system SURFER and was represented in the form of EMHGL isolines. The calculation method is the same as the one used for the current map ‘Groundwater Levels’ (Hannappel, Hörmann & Limberg 2007).

Further information about this

back to top of page